leetcode 765 - Couples Holding Hands

leetcode 765 - Couples Holding Hands

A Union-Find solution

We first assign groups to elements in the array.

For example, given array [2, 1, 5, 0, 3, 4], we assign groups as the following:

  • [0, 1]: group 0
  • [2, 3]: group 2
  • [4, 5]: group 4

To get the group number for a given array element, we can use arr[i] & (~0x1).

As a result, if we represent [2, 1, 5, 0, 3, 4] in group labels, we get [2, 0, 4, 0, 2, 4].

We visualize each group as a vertax of a undirected graph.

The initial connection of these vertaxes are determined by the pairs in the given array.

For example, if the array is [0, 0, 2, 2, 4, 4], we get the following graph:

graph 0

If the array is [2, 0, 4, 0, 2, 4], we get:

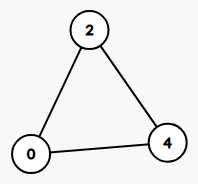
graph 1

Assume the size of the input array is N, If all the couples are seat next to each other, we want the graph to have exactly N / 2 connected components as shown in the [0, 0, 2, 2, 4, 4] graph.

After we convert the input array into an undirected graph, we convert the problem to:

Given this undirected graph with (N / 2) vertices, and at most two edges for a vertex, what is the minimum swaps needed to convert this graph to a graph that has exactly (N / 2) connected components?

We can observe that, for the given kind of graph, every swap is guaranteed to break one vertex free if it is in a connected component, and thus, increase the total number of connected component by 1.

For example, for the array [2, 0, 4, 0, 2, 4], after we swap idx 0 with idx 3, we get [0, 0, 4, 2, 2, 4]. By doing this, we break vertex 0 free, and increase the connected component count from 1 to 2.

As a result, we can conclude that (the # of components we increased) == (the # of swaps we have to do)

Our gaol is to increase the total number of components to N / 2. Thus we have (origional # of components) + (# of components we have to increase) == N / 2.

As a result, we have:
(# of swaps we have to do) == (# of components we have to increase) == N / 2 - (origional # of components)

So, the problem now is converted to find (origional # of connected components) in this undirected graph.

In order to find the origional number of connected components, we can do the following:

If we start with N / 2 connected components, each time we find a new edge between two components, we have to reduce the number of our connected components by 1.

For example, for array [0, 2, 2, 0, 4, 4], we should have 2 connected components: 0 - 2 and 4. If we start our component count at 3, when we see the first pair [0, 2], we know that component 0 and 2 are connected, so we reduce our component count to 2. Then, we see pair [2, 0], but since we already handled [0, 2], we don’t have to handle [2, 0] again since the graph is undirected. So, in the end, we find out that we have 2 connected components in the graph generated by [0, 2, 2, 0, 4, 4].

To achieve this, we can use Union-Find method.

We inspect one pair every time. If the two elements are not already in one group, we know that a new edge is now being added, which means we have to decrease the count of our connected components by 1. Then, we union these two groups.

The implementation is as following:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
int minSwapsCouples(vector<int>& row) {
    unordered_map<int, int> hm;
    for(int i = 0; i < row.size(); i ++) {
        // Assign group label to couples.
        // 0 1: 0
        // 2 3: 2
        // 4 5: 4
        // ...
        hm[row[i]] = row[i] & (~0x1);
    }

    // For each pair, if they are in two groups, we union the two groups together.
    // Every time we do a union, we have one less connected components.
    // The maximum number of connected components we can have is the number of couples, which is row.size() / 2.
    int maxNumOfConnectedComps = row.size() / 2;
    int initConnectedComps = maxNumOfConnectedComps;
    for(int i = 0; i < row.size(); i += 2) {
        int g1 = uf_find(hm, row[i]);
        int g2 = uf_find(hm, row[i + 1]);
        if(g1 != g2) {
            uf_union(hm, g1, g2);
            initConnectedComps --;
        }
    }
    // Now, initConnectedComps represents the number of connected components we have.
    // # of swaps needed = max # of connected components - # of connected components we have.
    // This is because in a given connected component, for each swap, we can at most generate one additional connected component.
    // So, # of swaps needed + # of connected components we currently have = max # of connected components.
    return maxNumOfConnectedComps - initConnectedComps;
}
void uf_union(unordered_map<int, int>& hm, int g1, int g2) {
    hm[g2] = g1;
}
int uf_find(unordered_map<int, int>& hm, int val) {
    if(hm[val] == val) {
        return val;
    } else {
        return uf_find(hm, hm[val]);
    }
}